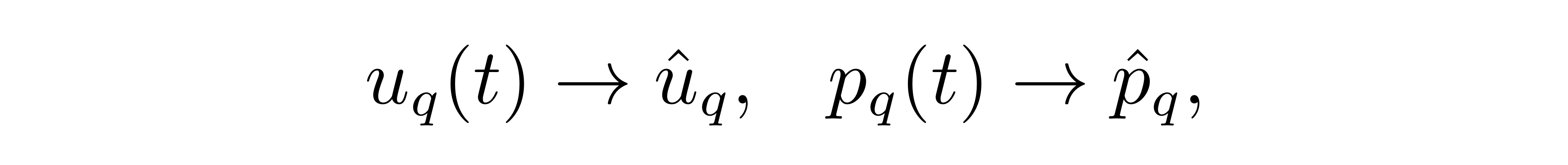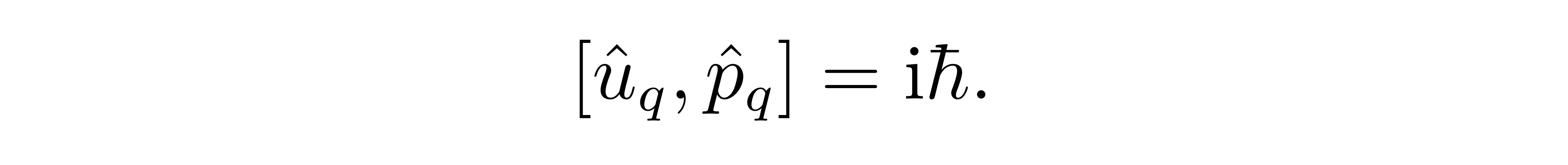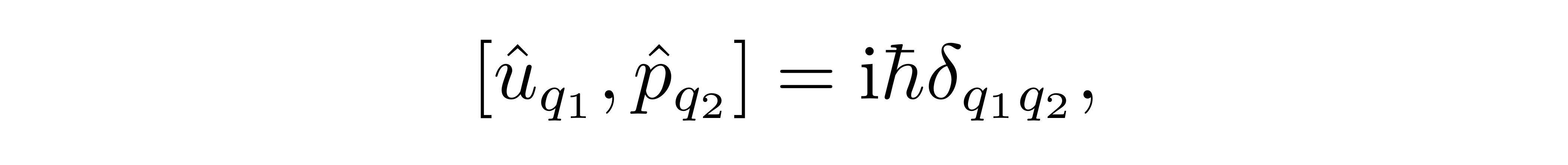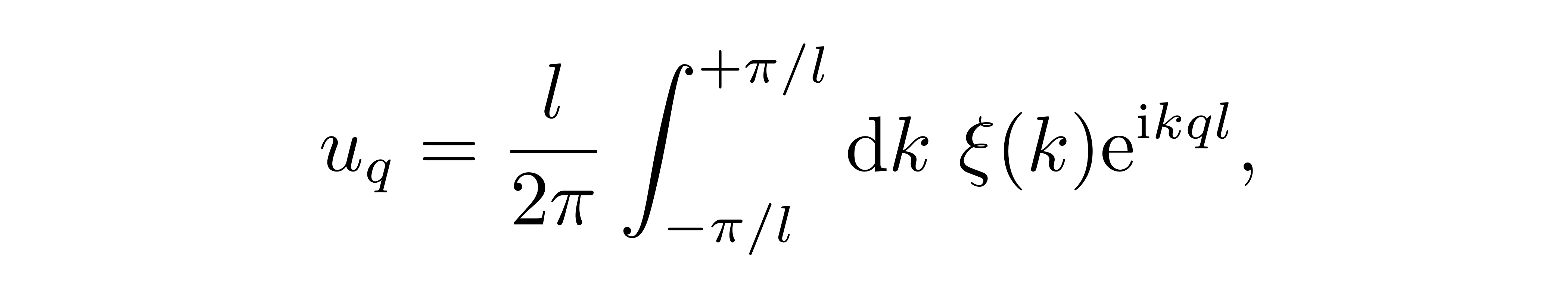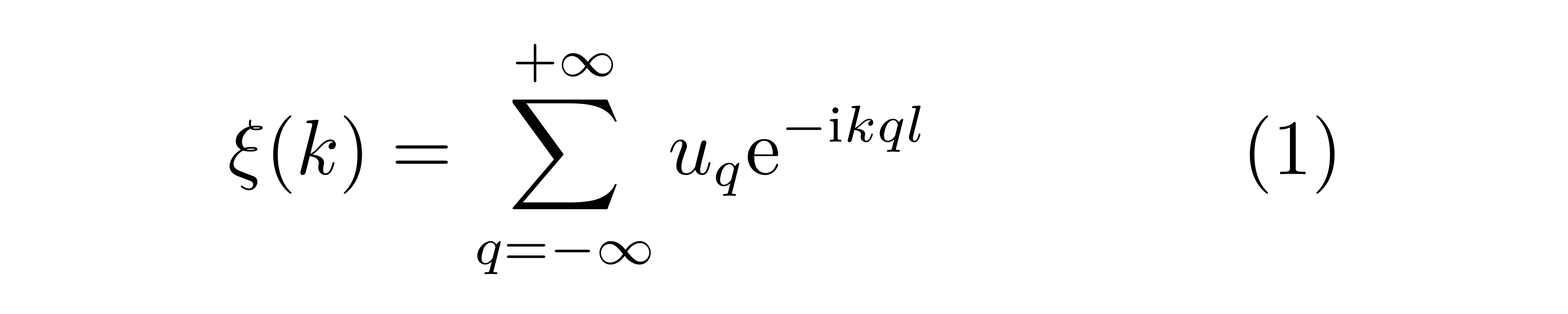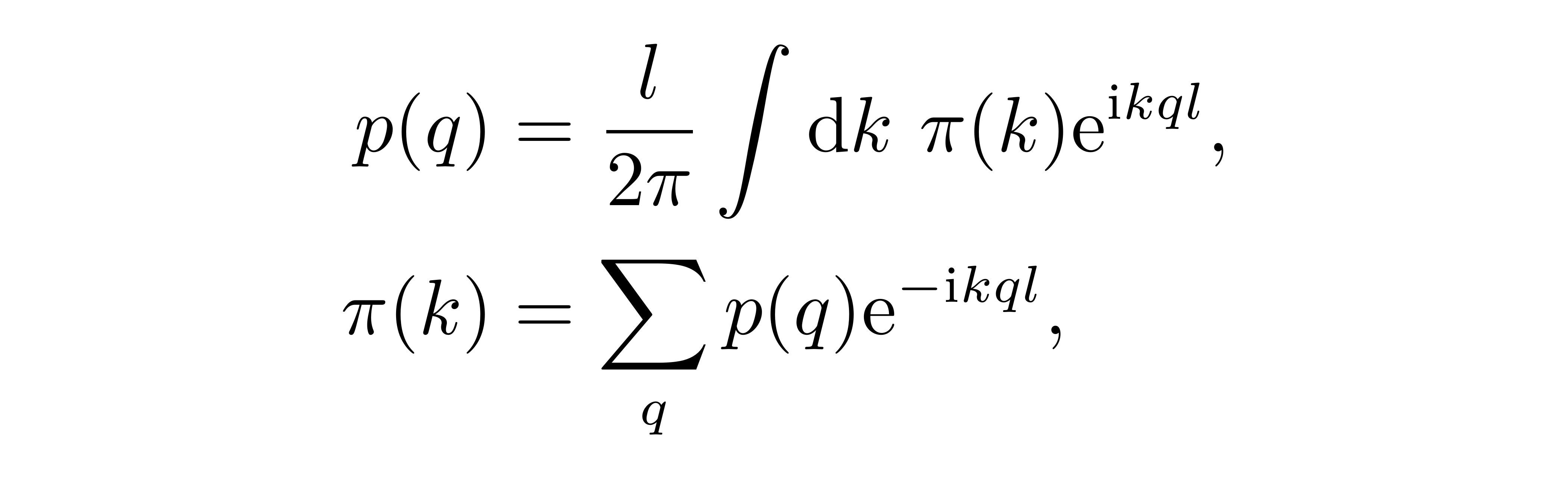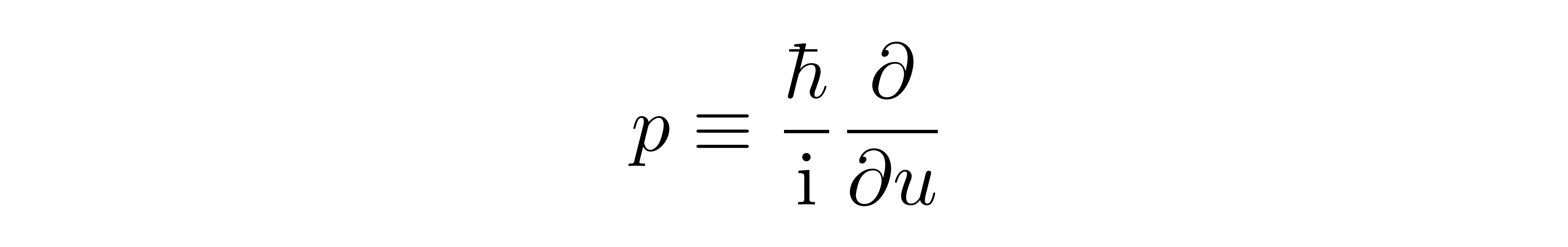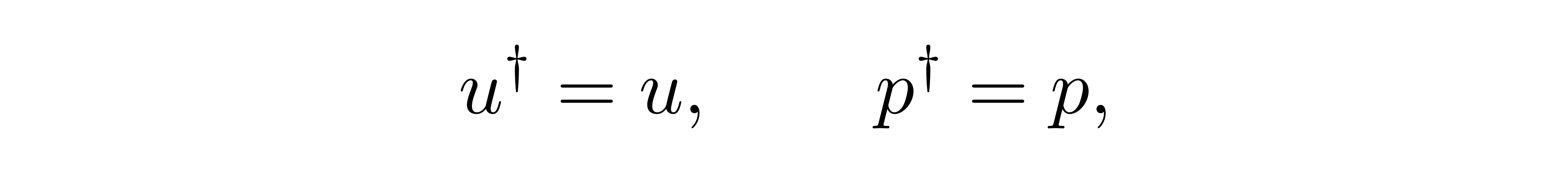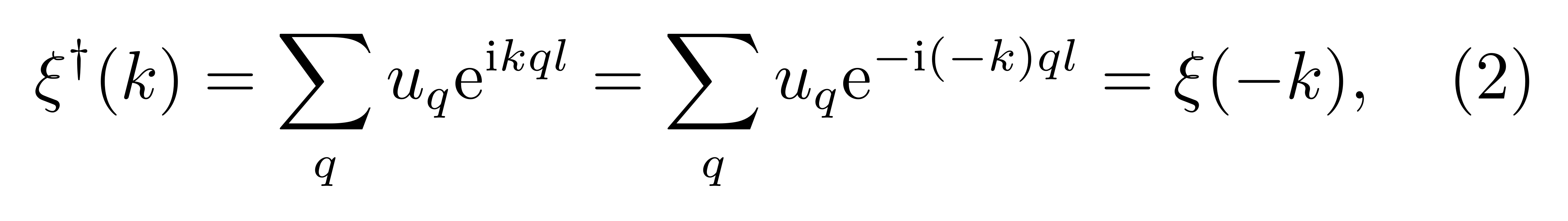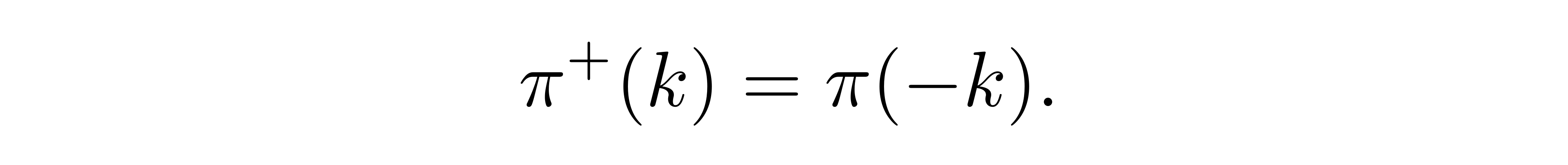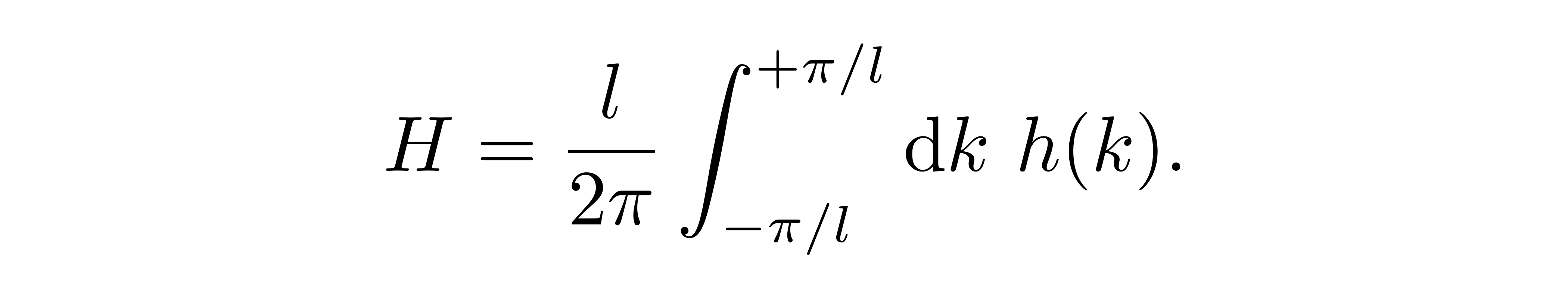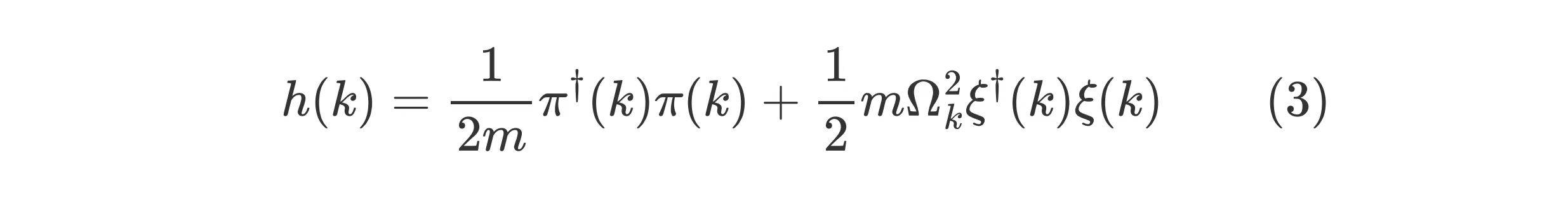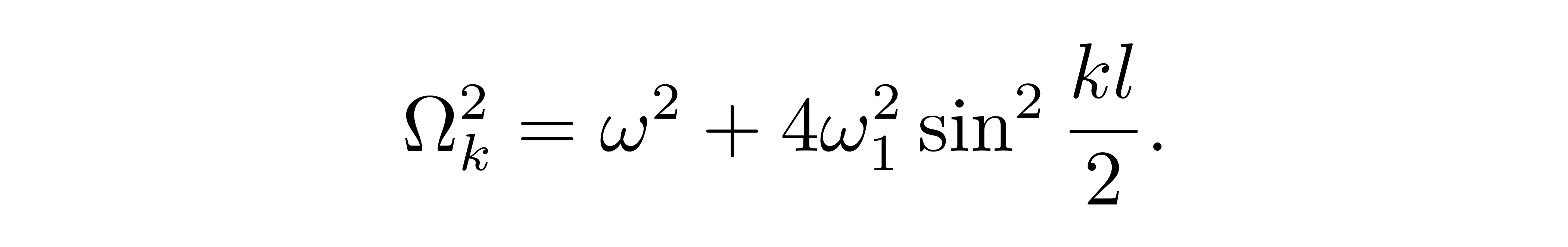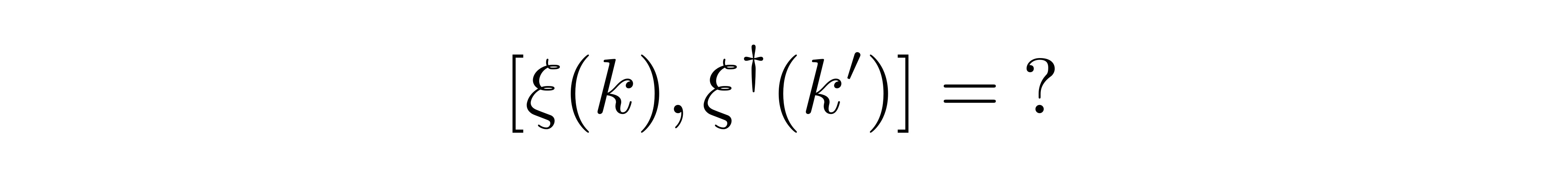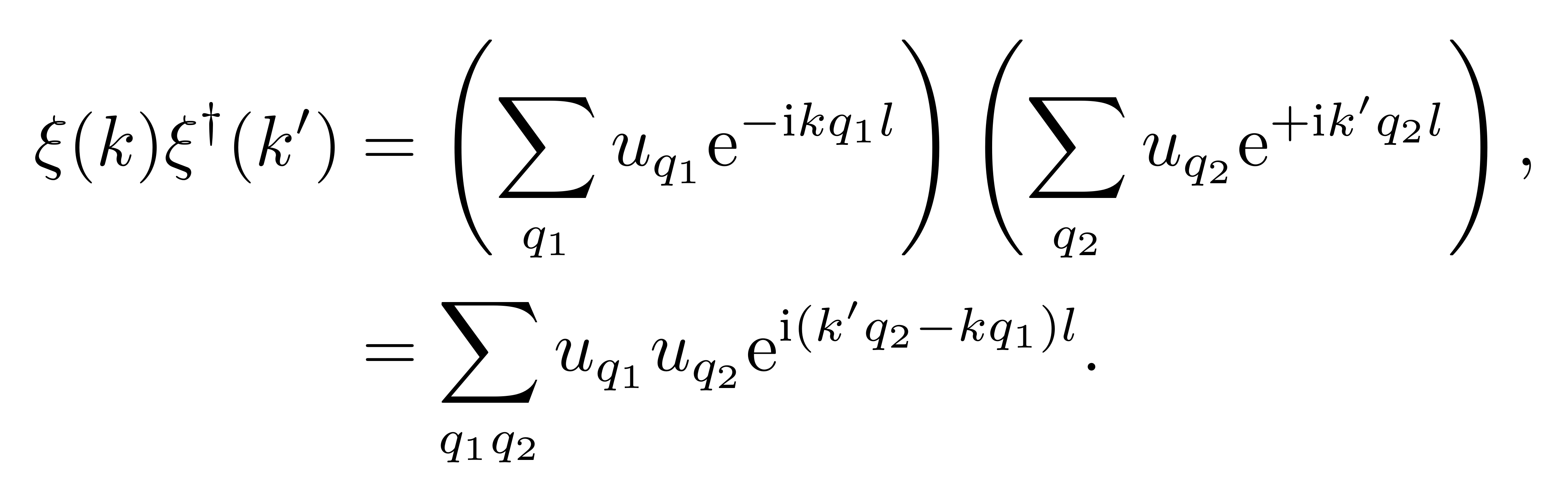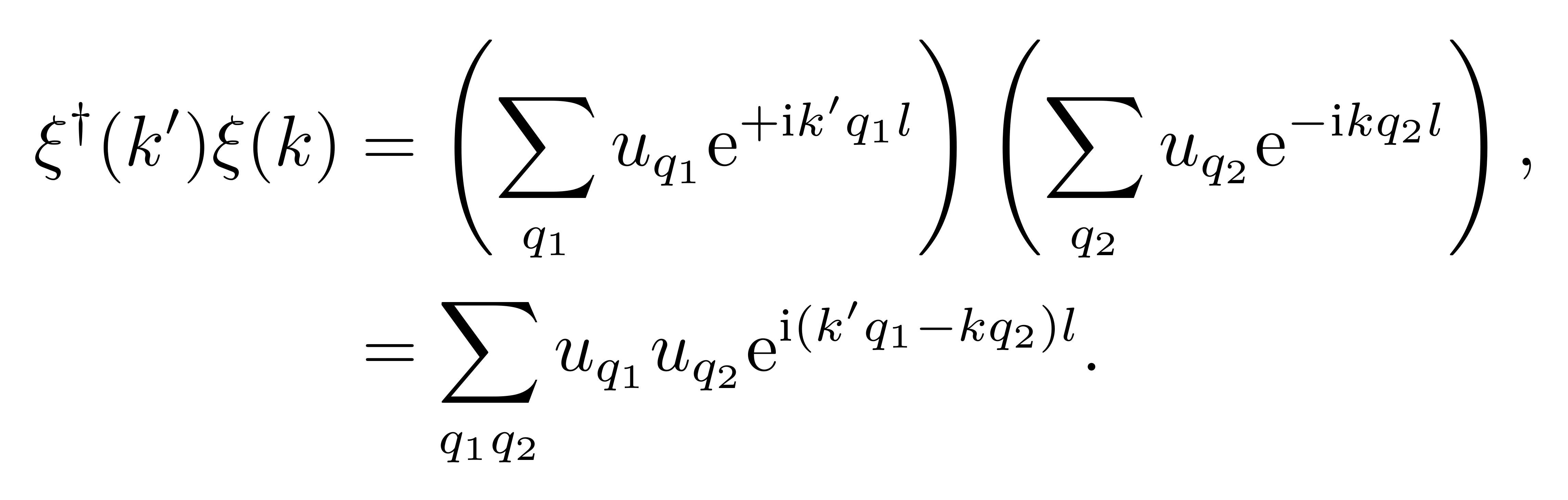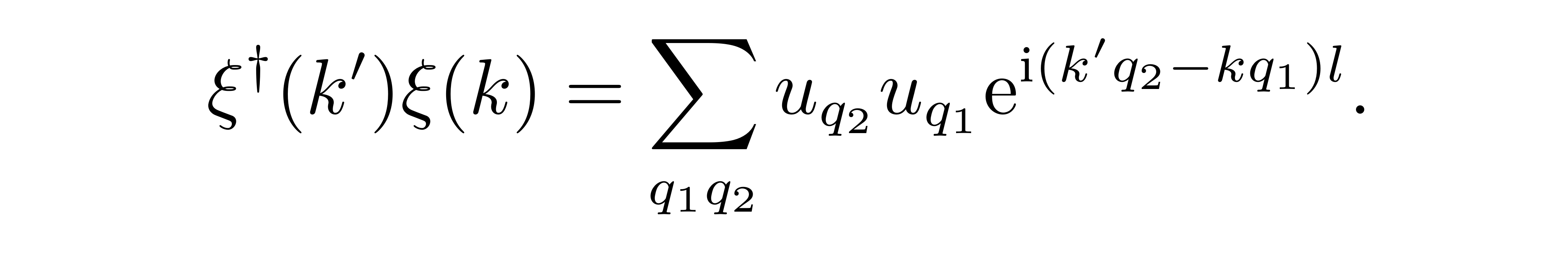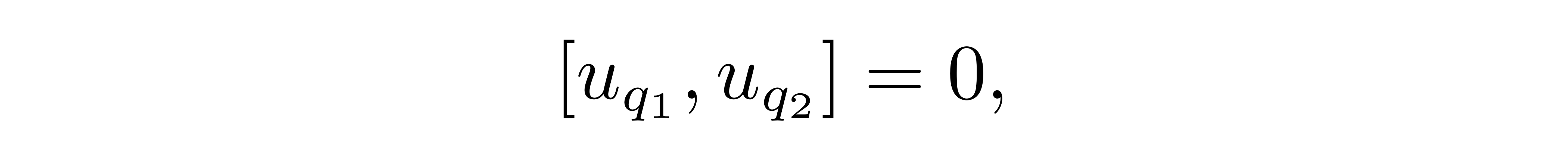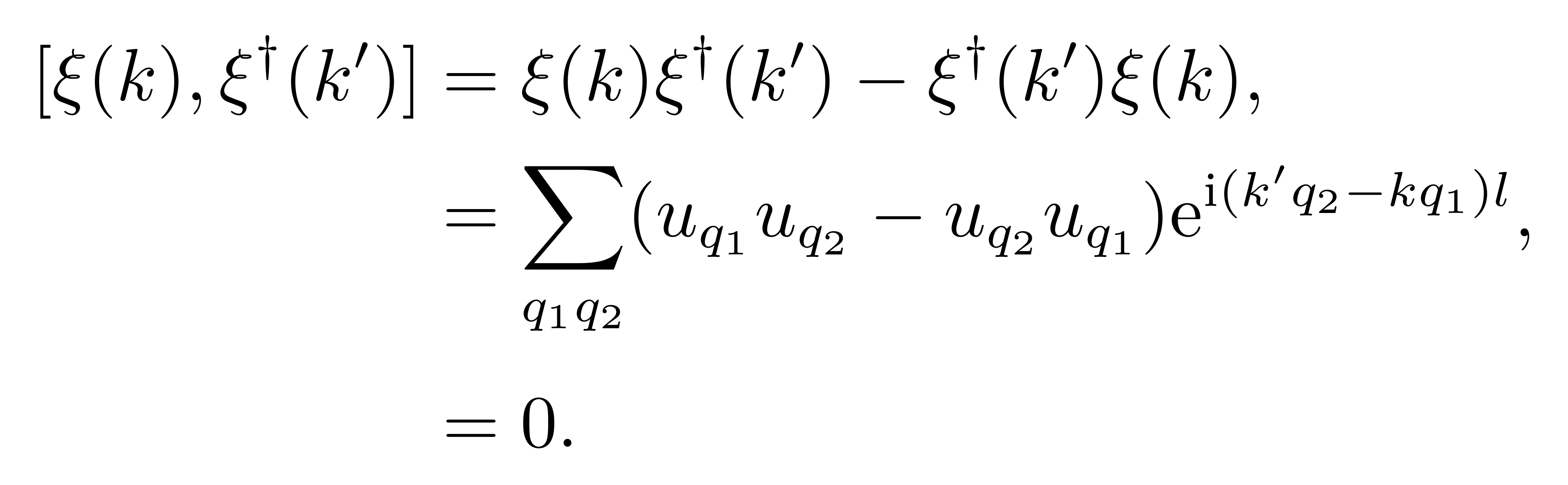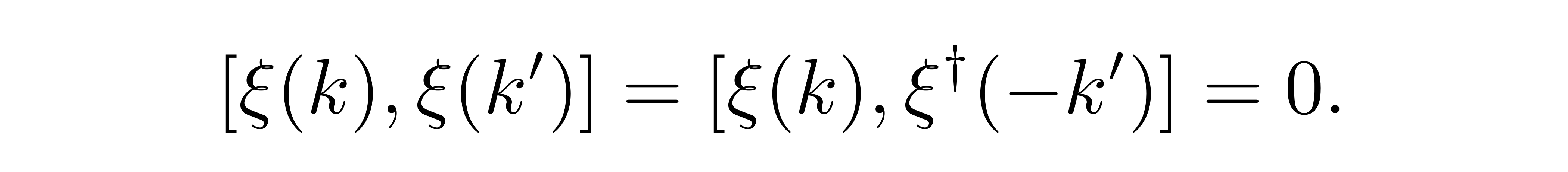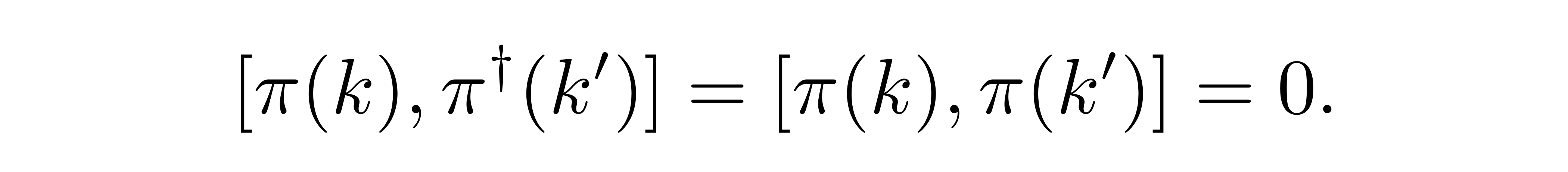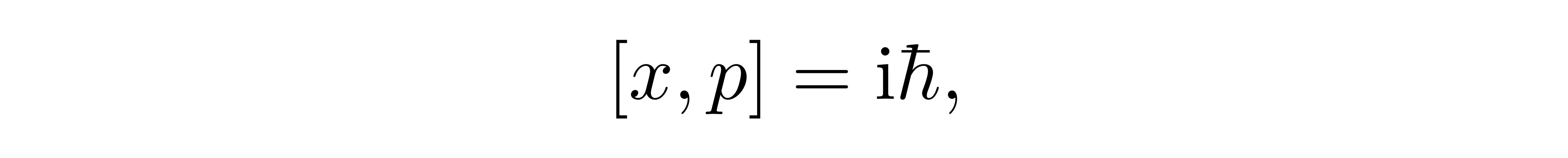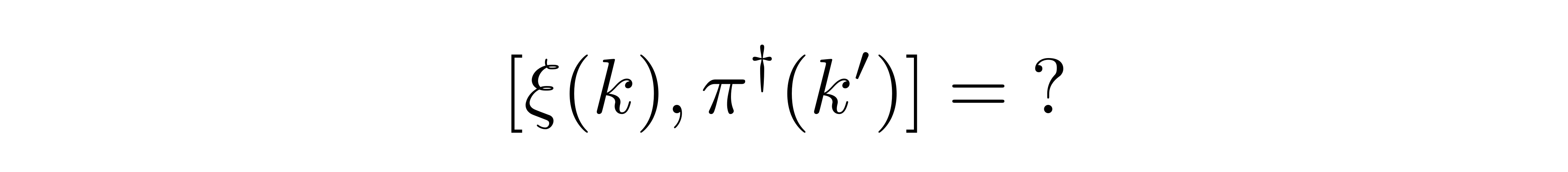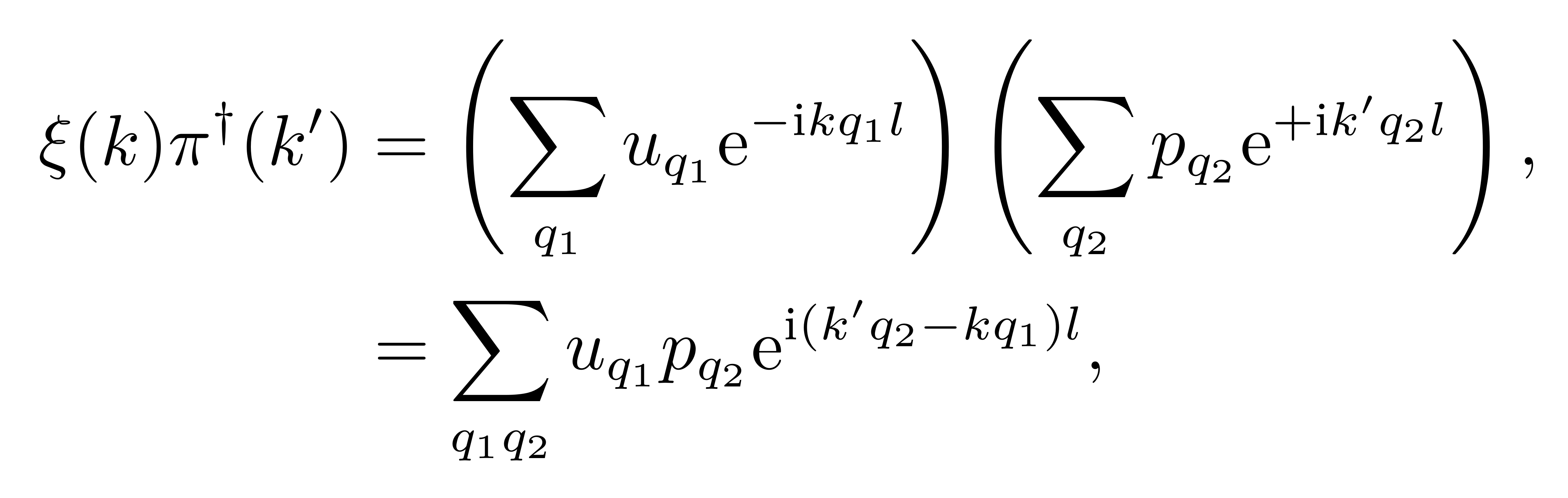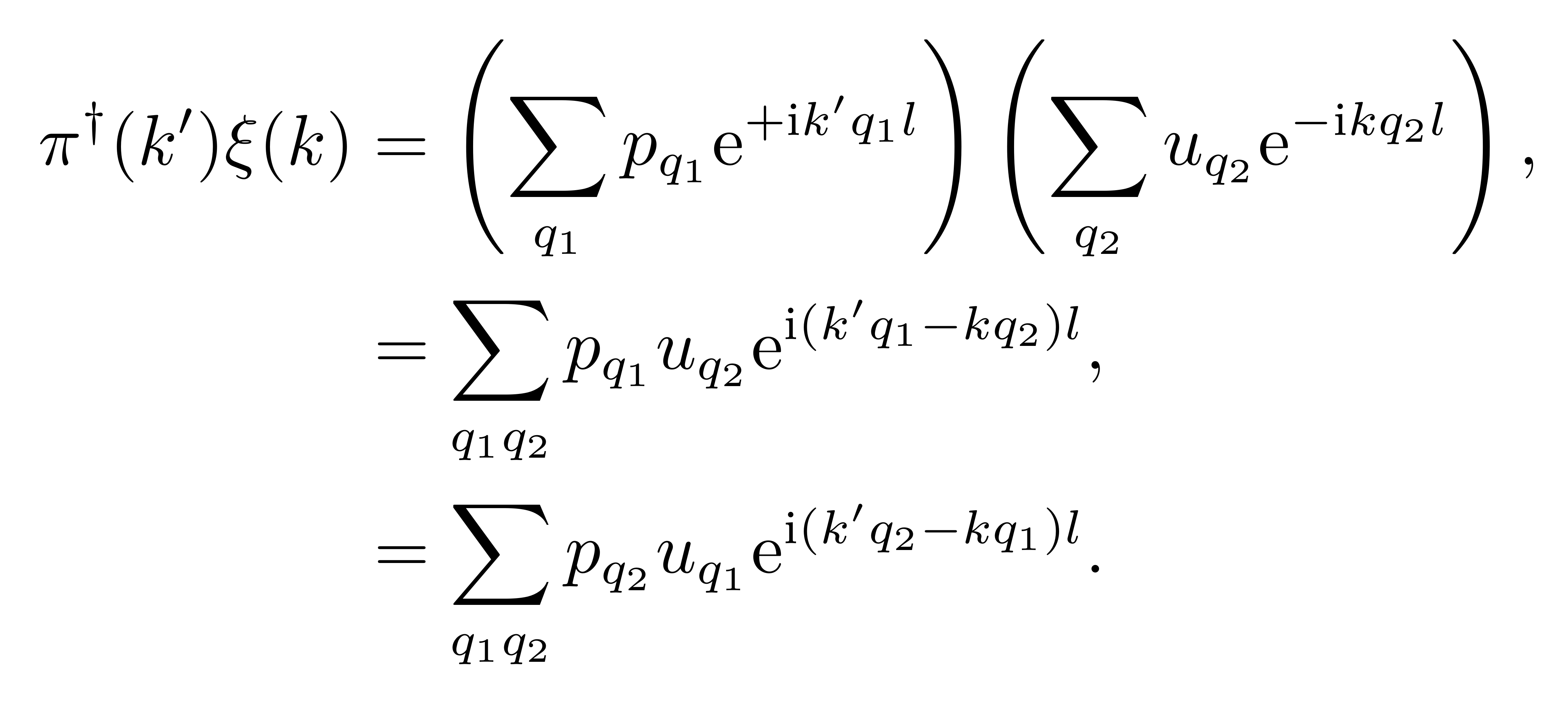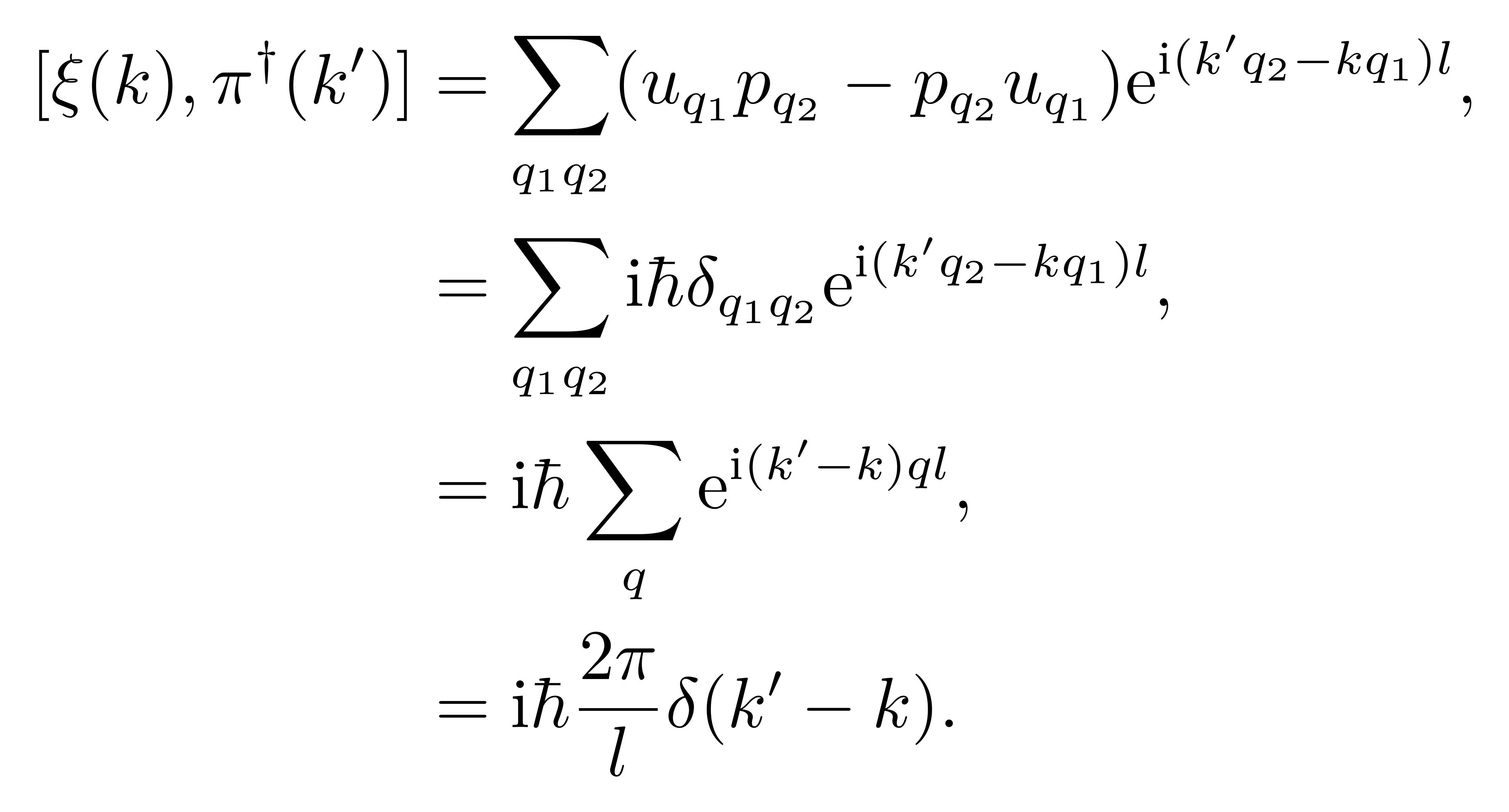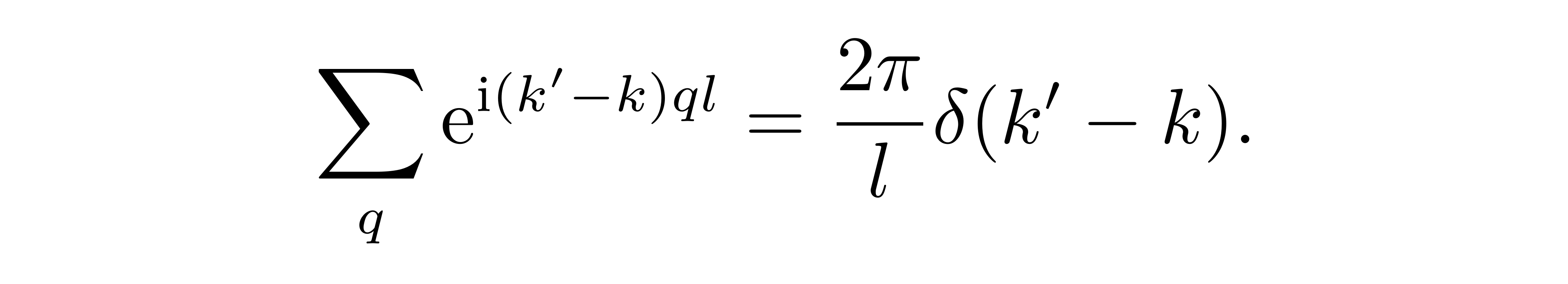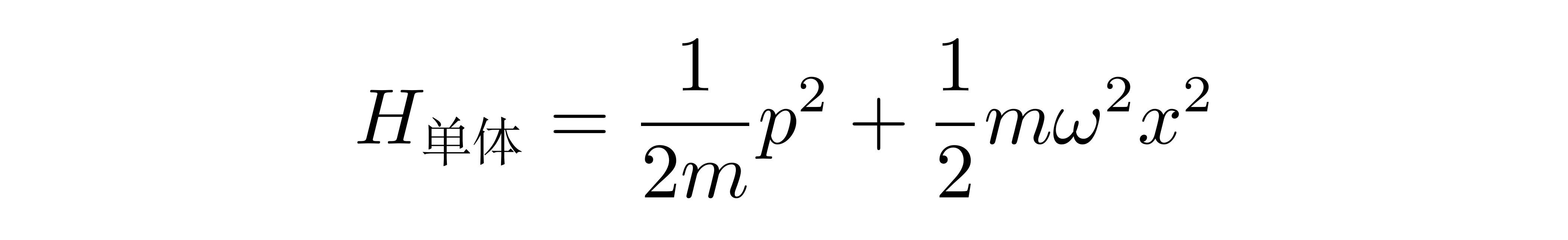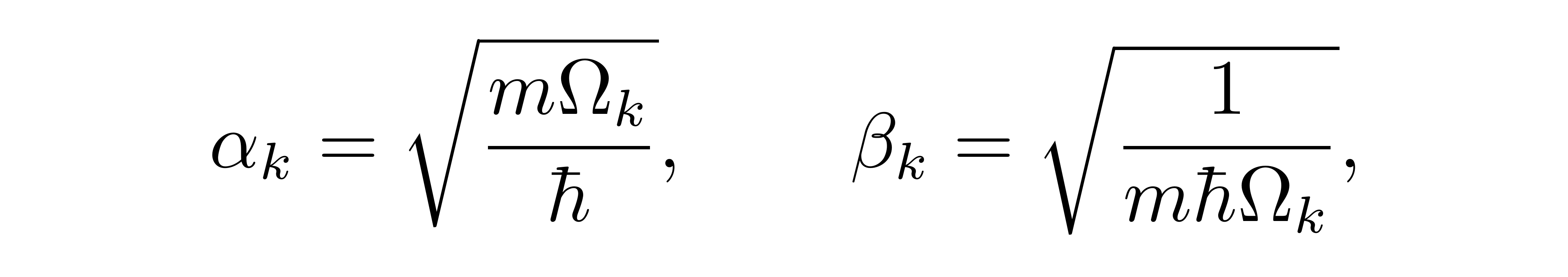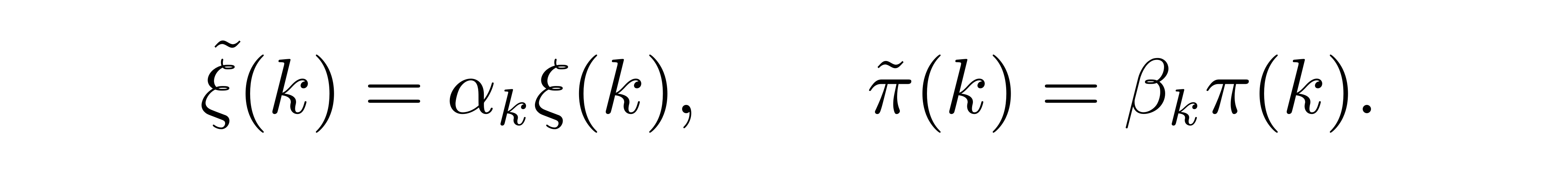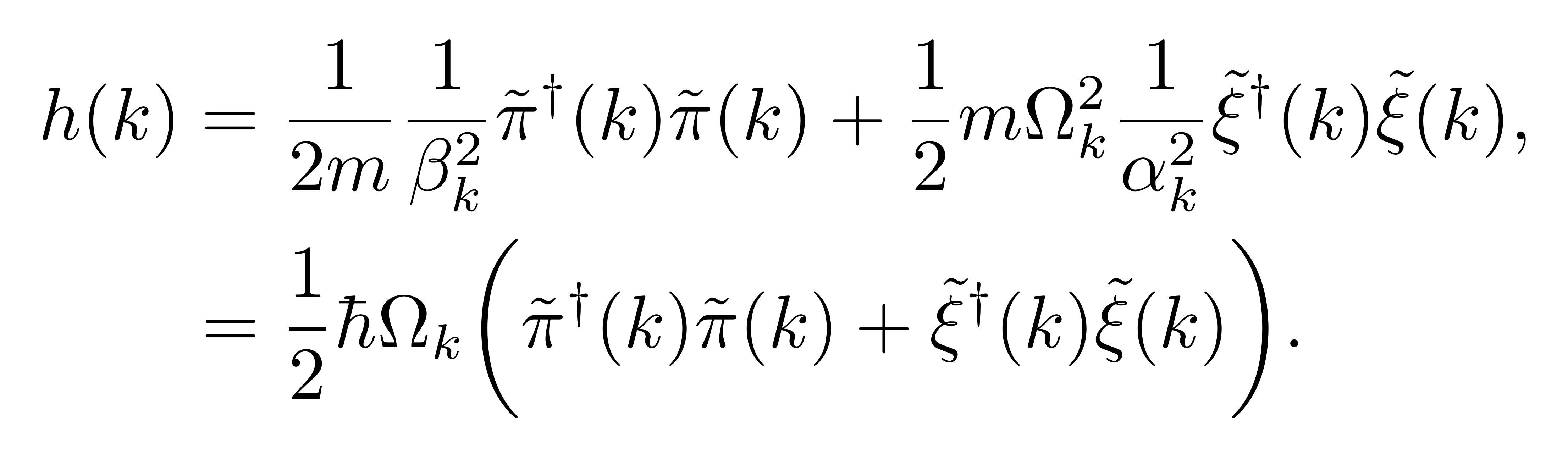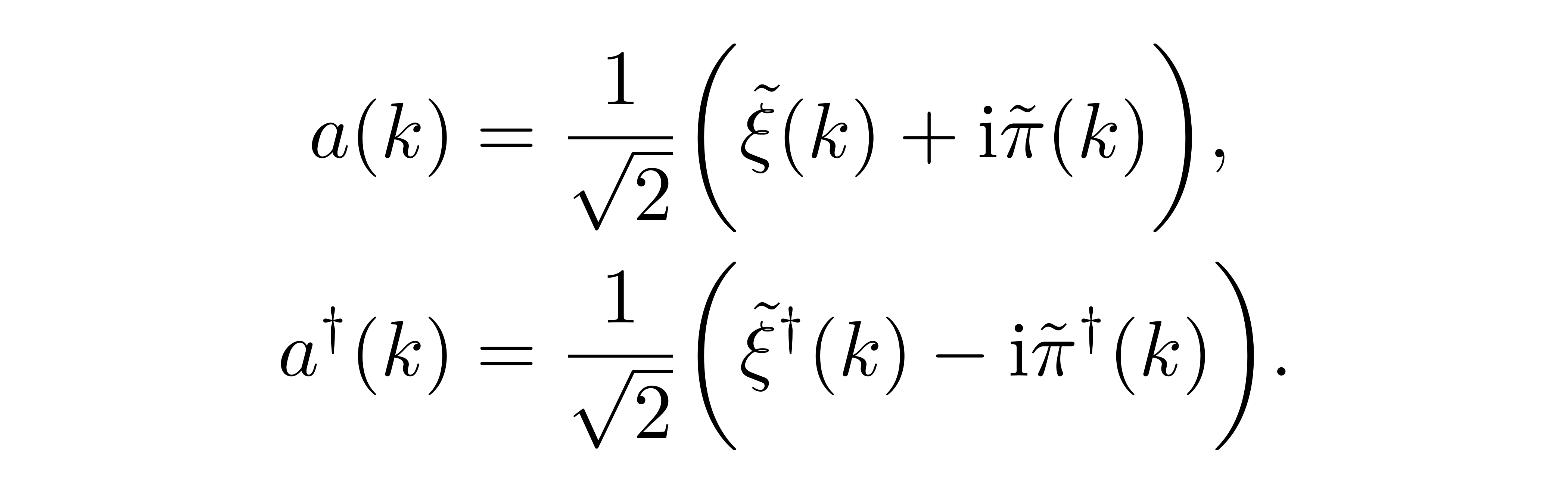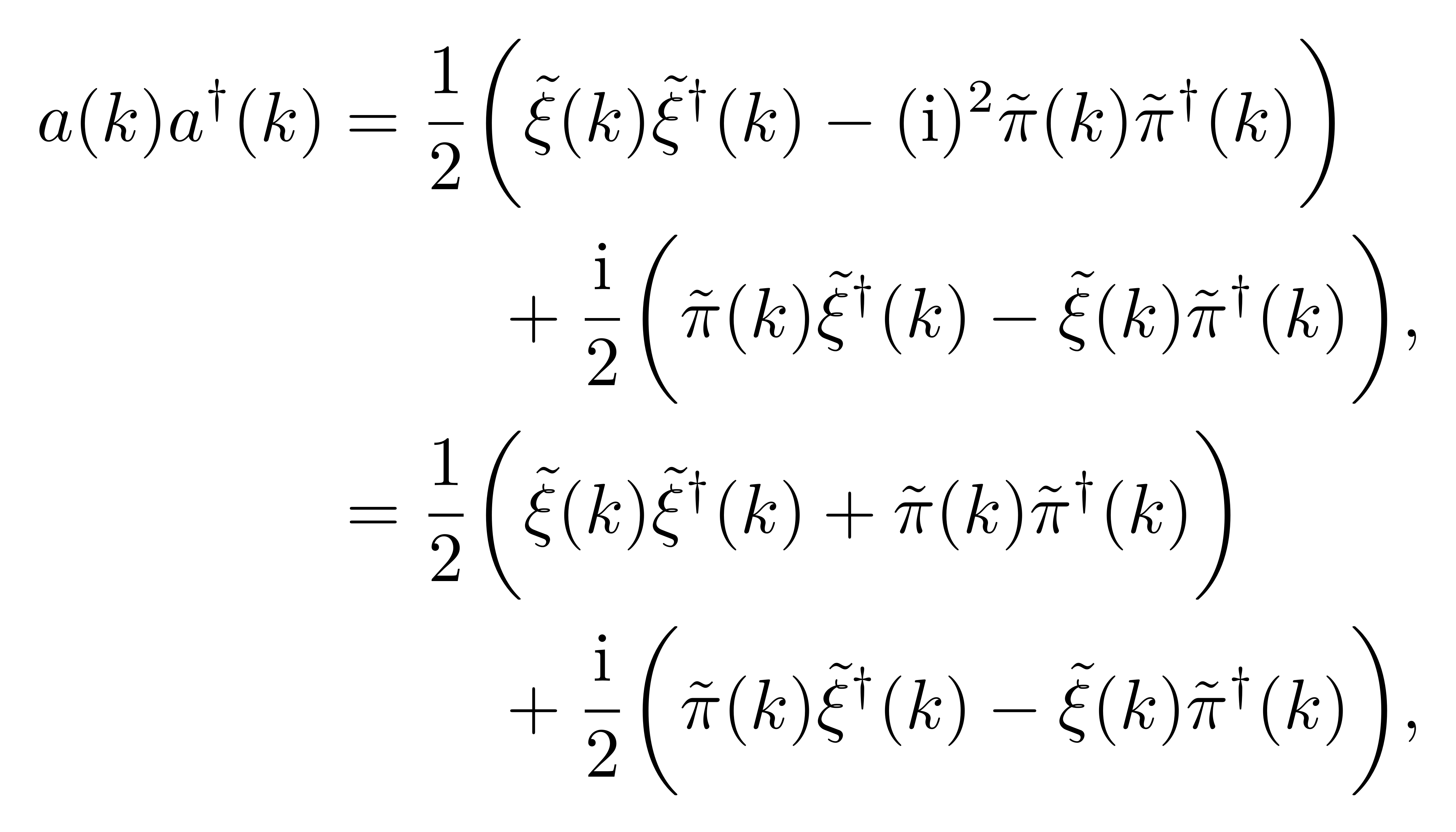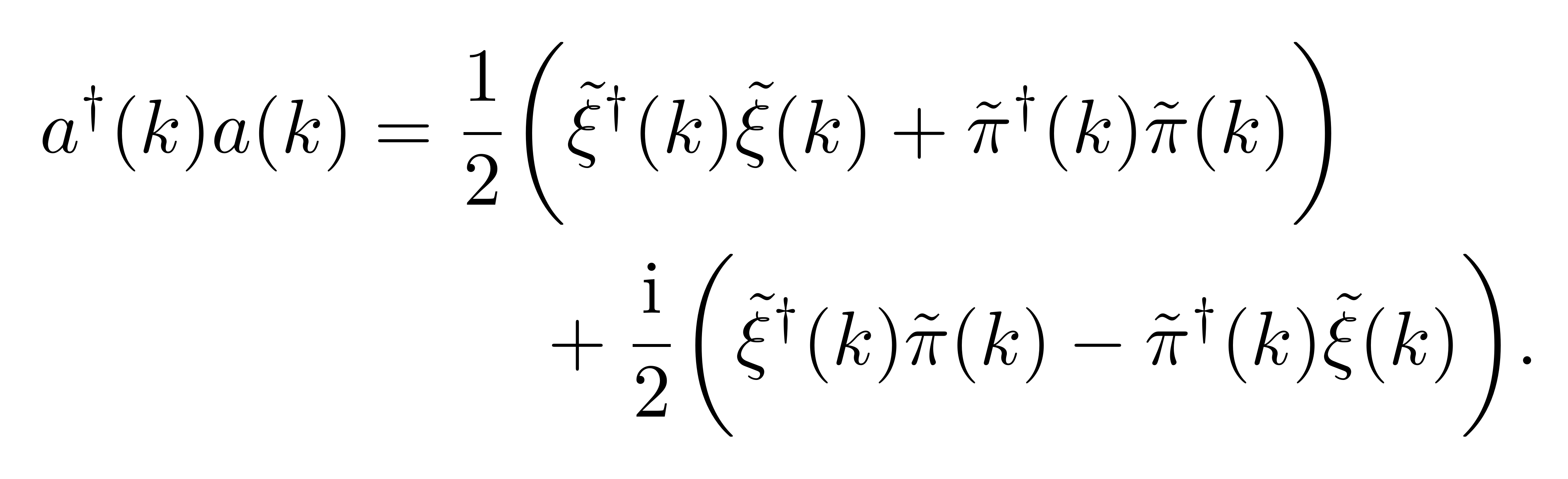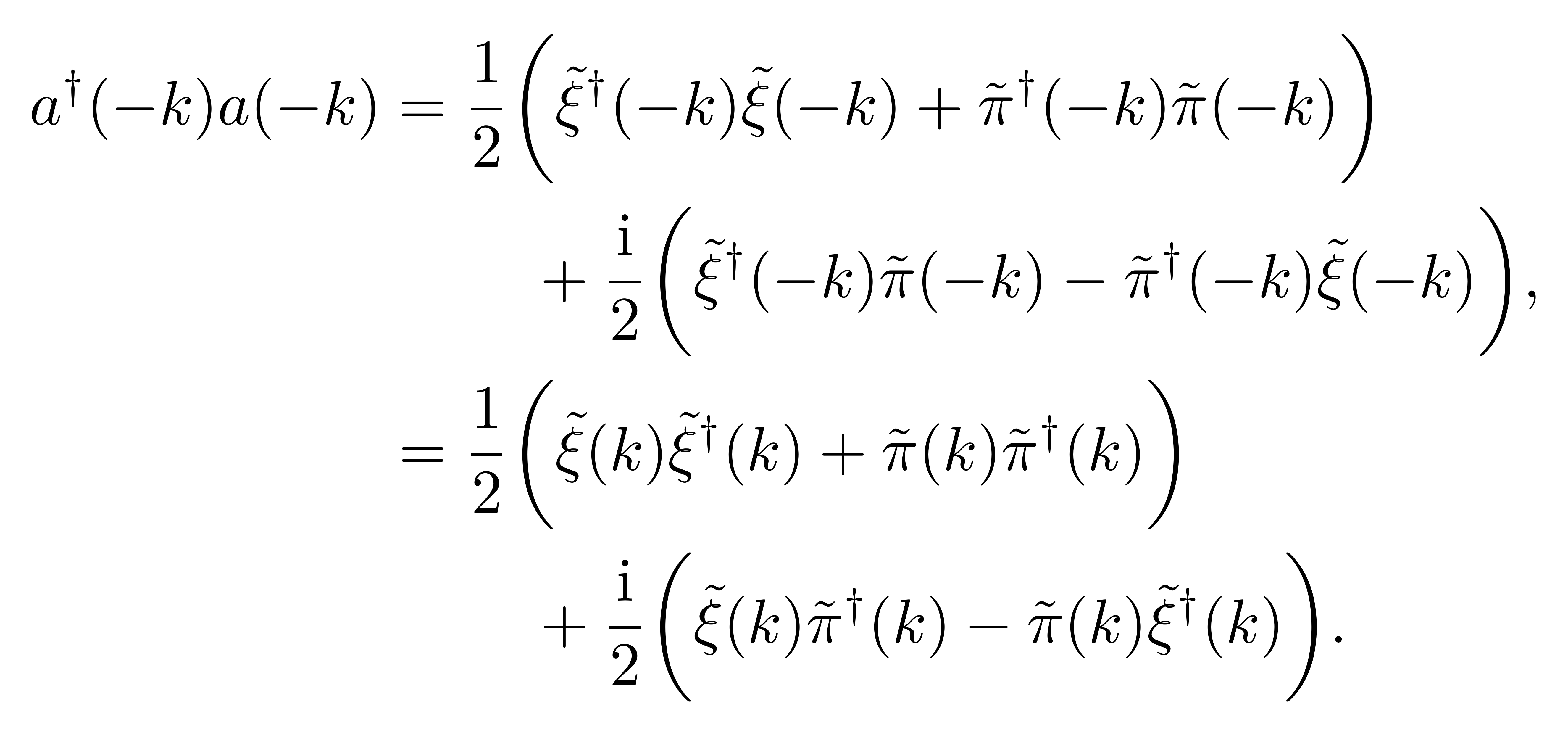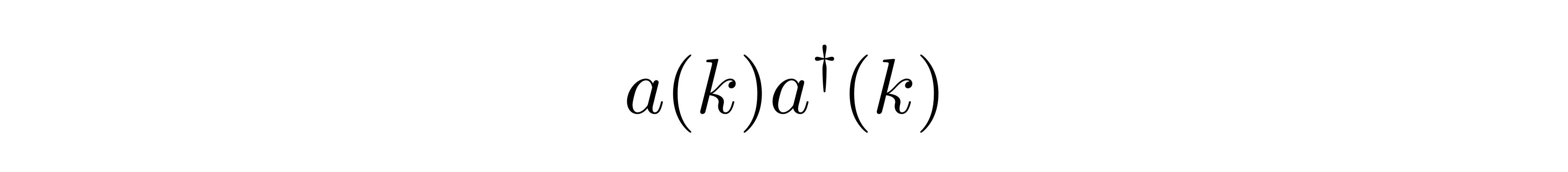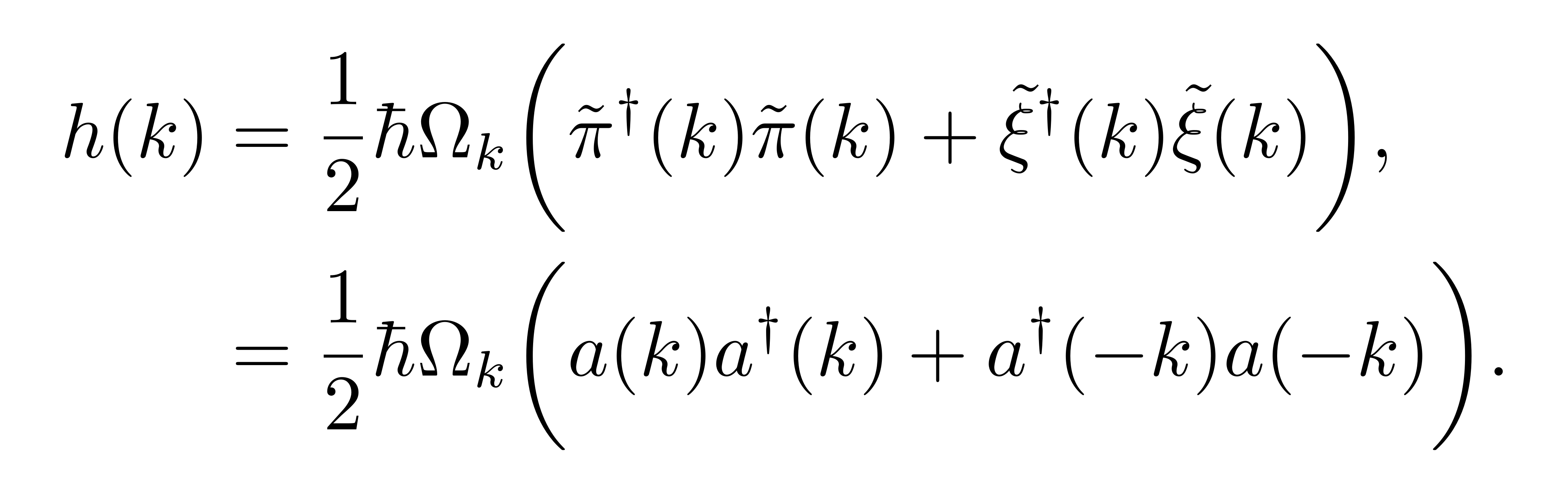habesha sports betting

并要求他们之间满足正则对易关系

值得注意的是，在算符化后，某一力学量算符定义不应再依赖于时间。同时，为了行文简洁和增加可读性，我们约定，在下文展开对量子化的谐振子链讨论中，都将略去对算符的 hat 记号。

考虑一条链上的不同点处的谐振子应该保持独立，于是考虑两点 q1 与 q2 时，上述对易关系又可以统一地被表达为

其中我们用到了Kronecker-δ记号。为了更好地求解体系的能谱，我们可以将格点傅里叶变换用于对算符的处理上，即取

或者利用其逆变换定义一个新的“坐标”算符

作为体系的基本自由度。形象地说，前者说明 u_q 相当于 ξ(k) 在投影到某个简正模式上的投影系数；或者从后者理解， 想象指数部分是一个“吸血鬼”，在每点的振荡模式 u_q 上都分别吸一点血，然后重新组合出 ξ(k) 。同样地，可以证明对正则动量同样有

这里格点傅里叶变换中的积分与求和的上下限与上面应当保持一致。同样是为了行文简洁，在不致混淆时，此后我们约定凡出现积分求和处，上下限将保持一致而略去不写。

张朝阳提醒，这里值得注意的是，作为可观测量的谐振子偏移量 u 及其正则动量

都是厄米算符

而经由傅里叶变换定义的辅助变量出现的 ξ(k) 则不然。利用式 (1) 不难验证

即其并非再是厄米算符，反而取共轭这一操作等价于将一个前向传播的波形（k > 0），转变为一个反向传播的波形（k < 0）。对 π 亦可得到同样的结论

以 ξ 和 π 为自由度下，或者说在“k空间”中，可以将哈密顿量改写为若干独立的振动模式的叠加

其中，每一独立振动模式的哈密顿量为

参数

为了在“k空间”中完成量子化，接下来要问是：这样一组新变量的对易关系为何？由于 ξ 的非厄米性，且注意到在哈密顿量中，ξ 与其厄米共轭一般成对出现，所以首先我们要问

具体的证明需要利用到展开式 (1)，仔细地计算不难得到

而另一方面，如果交换两算符的乘积顺序，

注意到交换下标 q1 和 q2 不会改变求和结果，所以又有

而由于不同位置处的 u 算符本身是对易的

即交换乘积顺序不改变结果，所以有

再利用 ξ 本身的性质（参见式 (2)），不难得到

同样的计算过程可以证明到

同时，类比于讨论单个谐振子中常用到的对易关系

我们还需要问

分别计算

和

注意此时指数部分是一致的，两者相减有

计算中，我们再次利用到了公式

张朝阳提醒，这里计算对易关系得到的是一个Dirac-δ函数。同一个模（k = k’）的“位移”、“动量”算符是不对易的，但是结果取到的不是 1 而是无穷大，它反映了参数 k 取值的连续性。

（张朝阳计算“k空间”中各力学量的对易关系）

以升降算符表达的哈密顿量

让我们重新回到单个模式的哈密顿量（参见式 (3)）。将其与单个谐振子的哈密顿量

相比，它们同样具有动量、坐标平方和的形式。同时，坐标及其对应正则动量之前不对易。这提示我们，类比对单个谐振子的处理，我们能否利用变量 ξ 和 π 定义单个模式的升降算符，以将哈密顿量写成物理意义更明确的形式？

为了定义升降算符，我们首先要对相关变量作无量纲化。引入两个常量

以重定义

于是单个模式的哈密顿量 (3) 可以重写为

这提示我们可以考虑定义

注意到

以及

注意到，由于算符 ξ 和 π 的非厄米性，计算结果中的交叉项不能通过简单的两式加减相消掉——这与对单个谐振子的讨论有本质的差异。

幸运的是，利用共轭关系 (2)，有

可以观察到此结果中的第一项

的第一项相同，而两者的交叉项恰好相差一个负号。于是，可以将给定参数 k 的某一模式的哈密顿量以升降算符改写为

而整个谐振子链的哈密顿量即是其积分。

（张朝阳以升降算符改写谐振子链的哈密顿量）

据了解，《张朝阳的物理课》于每周五、周日中午12时在搜狐视频直播，网友可以在搜狐视频APP“关注流”中搜索“张朝阳”，观看直播及往期完整视频回放；关注“张朝阳的物理课”账号，查看课程中的“知识点”短视频；此外，还可以在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详细文章。

500 piece crown casino clay poker chip jp commerce win win sport betting south sudan best sports betting app

---

声明：该文观点仅代表作者本人，搜狐号系信息发布平台，搜狐仅提供信息存储空间服务。